- Definisi Struktur Data Tree ( Pohon )
Pada kesempatan hari ini saya akan membahas tentang Struktur Data Tree ( Pohon ). Dalam ilmu komputer, Tree ( pohon ) sering digunakan oleh tipe data abstrak ( ADT ) atau mengimplementasikan stuktur data ADT yang mensimulasikan hirarkis struktur pohon , dengan nilai akar dan sub pohon dari anak-anak, direpresentasikan sebagai satu set node yang terhubung. Sebuah struktur data pohon dapat didefinisikan secara rekursif ( lokal ) sebagai kumpulan node ( mulai pada simpul akar ), di mana setiap node adalah struktur data yang terdiri dari nilai, bersama dengan daftar referensi ke node ( "anak-anak " ), dengan kendala-kendala yang ada referensi diduplikasi, dan tidak ada poin ke akar. Atau, pohon dapat didefinisikan secara abstrak secara keseluruhan ( global ) sebagai pohon memerintahkan, dengan nilai yang diberikan ke setiap node. Kedua perspektif ini berguna : sementara pohon dapat dianalisis secara matematis secara keseluruhan, padahal sebenarnya direpresentasikan sebagai struktur data biasanya diwakili dan bekerja dengan terpisah oleh simpul ( bukan sebagai list node dan kedekatan list dari tepi antara node, sebagai salah satu mungkin merupakan digraph, misalnya ). Misalnya, melihat sebuah pohon secara keseluruhan, seseorang dapat berbicara tentang " node induk " dari node yang diberikan, tetapi secara umum sebagai struktur data node yang diberikan hanya berisi daftar anak-anak, tetapi tidak mengandung referensi ke induknya ( jika ada).
Contoh penggunaan Struktur Tree ( Pohon ):
- Silsilah keluarga
- Parse Tree (pada compiler)
- Struktur File
- Pertandingan
Struktur Tree ( Pohon )
Operasi-operasi Pada Tree
- Insert: menambah node ke dalam Tree secara rekursif. Jika data yang akan dimasukkan lebih besar daripada elemen root, maka akan diletakkan di node sebelah kanan, sebaliknya jika lebih kecil maka akan diletakkan di node sebelah kiri. Untuk data pertama akan menjadi elemen root.
- Find: mencari node di dalam Tree secara rekursif sampai node tersebut ditemukan dengan menggunakan variable bantuan ketemu. Syaratnya adalah tree tidak boleh kosong.
- Traverse: yaitu operasi kunjungan terhadap node-node dalam pohon dimana masing-masing node akan dikunjungi sekali.
- Count: menghitung jumlah node dalam Tree.
- Height : mengetahui kedalaman sebuah Tree.
- Find Min dan Find Max : mencari nilai terkecil dan terbesar pada Tree.
- Child : mengetahui anak dari sebuah node (jika punya).
- Daun/leaf : Simpul yang derajat = 0 disebut daun / leaf
- Hubungan antar simpul : bapak, ,anak, paman, dll
- Tingkat (level)
- Derajat (degree)
- Tinggi (height)/kedalaman (depth) : height = tingkat maksimum – 1
- Ancestor : semua simpul yang terdapat pada lintasan/jalur dari akar sampai simpul tersebut
- Forest (Hutan) : kumpulan sejumlah pohon yang tidak saling berhubungan
Berdasarkan banyaknya anak :
- Binary tree / pedigree chart : Complete Binary Tree tingkat N, Skewed Binary Tree
- Non Binary Tree (N-ary) & Lineal Chart
- Ordered tree
- Non Ordered tree
Jenis Tranversal :
- PreOrder : cetak node yang dikunjungi, kunjungi left dan kunjungi right
- InOrder : kunjungi left, cetak node yang dikunjungi, kunjungi right
- PostOrder : kunjungi left, kunjungi right, cetak node yang dikunjungi
- Diagram venn
- Notasi Kurung
Type Infotype : . . . . . . . .{ terdefinisi }
Type address : . . . . . . . .{ terdefinisi, sesuai dengan representasi fisik }
Type node : < Info : Infotype,
Left: address ,
Right: address >
Type BinTree : address
Jika P adalah binary tree, maka
Left (P) : mendapatkan alamat cabang kiri dari P
right (P) : mendapat alamat cabang dari kanan dari P
info (P) : mendapatkan bagian info dari node yang ditunjuk P
- Implementasi pohon biner dalam C
Program berikut menunjukan bagaimanan membangun sebuah pohon biner dalam program C. Menggunakan alokasi memori dinamis, pointer sebuah pohon biner, sangat berguna dalam struktur data, karena memungkinkan penyisipan lebih efisien, pencarian dan penghapusan dalam daftar diurutkan. Sebagai pohon itu pada dasarnya adalah sebuah struktur yang didefinisikan secara rekursif, pemrograman rekursif adalah cara alami dan efisien untuk menanganinya.
- Algoritma Tanversal ( PreOrder, InOrder, PostOrder )
InOrde Non Rekursif
Procedure InOrder (Input P
: BinTree)
{I.S : Terdefinisi Binary Tree P, mungkin kosong }
{F.S : Mencetak informasi
yang disisipakan dalam binary tree P secara InOrder, non rekursif }
Kamus
S : Stack
Q : BinTree
Algoritama
If (
P = Nil ) then
Output ( ‘Tree Kosong’ )
Else
S ß Nil {
Inisialisasi Tunpukan }
Q ß P
Repeat
While ( P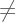 
Nil )
Nil )
{ bergerak terlebih dulu ke cabang
kiri dengan mempush akar }
Push ( S,Q )
Q ß Left ( Q )
{ P = Nil }
{ Mempop dan mencetak ujung tumpukan
}
Pop ( S,Q )
Output ( Info (Q) )
{ Bergerak ke kanan }
Q ß Right (Q) )
Until ( S =
Nil )
PostOrder Non Rekursif
Procedure PostOrder (
Input P : BinTree )
{ I.S : Terdefinisi Binary Tree P, mungkin kosong }
{ F.S : Mencetak
informasi yang disimpan dalam binary Tree P secara Inorder, non rekursif }
Kamus
S : Stack
Q : BinTree
Algoritma
If ( P = Nil ) then
Output ( ‘Tree Kosong ’ )
Else
S ß Nil {
Inisialisasi Tumpukan }
Q ß P
Repeat
If Q 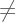Nil then
Nil then
While ( Q 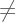Nil )
Nil )
{ bergerak terlebih
dulu kecabang kiri dengan mempush akar }
Push
( S,Q )
Q ß Left (Q )
{ Q = Nil }
Else
Pop ( S, Q )
Output ( Info (Q) )
Q ß top (S )
{ Bergerak ke kanan }
Q ß Right (Q)
Until
( S = Nil )
PreOrder Non Rekursif
Procedure PreOrder (
Input P : BinTree )
{ I.S : terdefinisi Binary Tree P, mungkin kosong }
{ F.S : Mencetak
informasi yang disimpan dalam binary Tree P secara PreOrder, non rekursif }
Kamus
S : Stack
Q : BinTree
Algoritma
If P = Nil then
Output ( ‘Tree Kosong’ )
Else
S ß Nil {
Inisialusasi tumpukan }
Push ( S, P ) {
push simpul akar }
While ( S <> Nil )
Pop (S,Q ) { Pop ujung tumpukan }
While Q
<> Nil
Output
( Info (Q) { kunjungan ke
simpul, cetak }
If ( Right (Q) ) 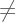Nil then
Nil then
{
ada cabang kanan, push ke stack }
Push
( S, Right (Q) )
Q ß Left (Q)
PreOrder Rekursif
Procedure
PreOrder_Rekursif ( Input P : BinTree )
{ I.S : terdefinisi Binary Tree P, P mungkin kosong
}
{ F.S : Mencetak
informasi yang disimpan dalam binary Tree P secara PreOrder, rekursif }
Algoritma
If ( P 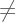Nil ) then
Nil ) then
Output ( Info (P) )
PreOrder_Rekursif (Left (P) )
PreOrder_Rekursif (Right (P) )
InOrder Rekursif
Procedure
InOrder_Rekursif (Input P : BinTree )
{ I.S : terdefinisi Binary Tree P, P mungkin kosong
}
{ F.S : Mencetak
informasi yang disimpan dalam binary Tree P secara InOrder, rekursif }
Algoritma
If ( P 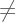Nil ) then
Nil ) then
InOrder_Rekursif (Left (P) )
Output ( Info (P) )
InOrder_Rekursif (Right (P) )
- Membentuk tree dan list PreOrder & InOrder
berikut script code program saya menggunakan C
#include <stdio.h>
typedef struct node{
char data;
node *left;
node *right;
};
node *root=NULL;
void Tambahnode(node **root, char isi) {
if((*root)==NULL){
node *baru;
baru= new node;
baru->data = isi;
baru->left = NULL;
baru->right = NULL;
(*root)=baru;
}
}
void preorder(node *root) {
if(root !=NULL) {
printf(“%c “, root->data);
preorder(root->left);
preorder(root->right);
}
}
void inorder(node *root) {
if(root !=NULL) {
inorder(root->left);
printf(“%c “, root->data);
inorder(root->right);
}
}
void postorder(node *root) {
if(root !=NULL) {
postorder(root->left);
postorder(root->right);
printf(“%c “, root->data);
}
}
main()
{
char kata;
printf(“Program By: AH. Husain Sidqi[A110904822]\n\n”);
Tambahnode(&root,kata=’S');
Tambahnode(&root->left,kata=’I');
Tambahnode(&root->left->left,kata=’D');
Tambahnode(&root->left->left->left,kata=’Q');
Tambahnode(&root->left->left->right,kata=’I');
Tambahnode(&root->right,kata=’H');
printf(“Tampilan secara PreOrder : “);
preorder(root);
printf(“\nTampilan secara InOrder : “);
inorder(root);
printf(“\nTampilan secara PostOrder : “);
postorder(root);
}
